Blog

New algorithmic frontiers.

Features authors & research from:

UC Berkeley MIT Stanford University Peking University Northwestern University University of Washington University of Pennsylvania University of Notre Dame TU Munich UCSF MIT-IBM Watson AI Lab IBM Research AMD Cerebras Pacific Northwest National Laboratory Lawrence Berkeley National Laboratory
How IBM Used OpenEvolve to Discover Quantum Error Correction Codes

How IBM Used OpenEvolve to Discover Quantum Error Correction Codes

IBM Research used OpenEvolve to search for new quantum error correction codes, evolving Python programs that generate bivariate bicycle code candidates - the code family at the heart of IBM's fault-tolerant quantum computing roadmap. Across five evolution campaigns totalling roughly 1,650 iterations, about 200,000 screened candidates, 140 hours of compute and around US$400 in LLM inference, the pipeline discovered 465 distinct candidate codes, including a weight-8 [[288,50,8]] code that encodes 50 logical qubits at certified distance 8 (the previously published weight-6 record was k = 16) and a new [[288,16,12]] code whose distance was certified exactly.
How AMD Used OpenEvolve to Optimise GPU Kernels

How AMD Used OpenEvolve to Optimise GPU Kernels

AMD-AGI Group adapted OpenEvolve to automatically optimize GPU kernels written in Triton for AMD Instinct™ GPUs. Our system, GEAK-OpenEvolve, uses OpenEvolve's population-based evolutionary framework enhanced with a Quality-Diversity search, hardware-specific prompt engineering, and a cascade evaluation pipeline. It achieves an average 3.42x speedup over reference kernels on the TritonBench-modified benchmark and a 7.02x speedup on our ROCm-bench suite.
OpenEvolve for Quasi-Monte Carlo Design

OpenEvolve for Quasi-Monte Carlo Design

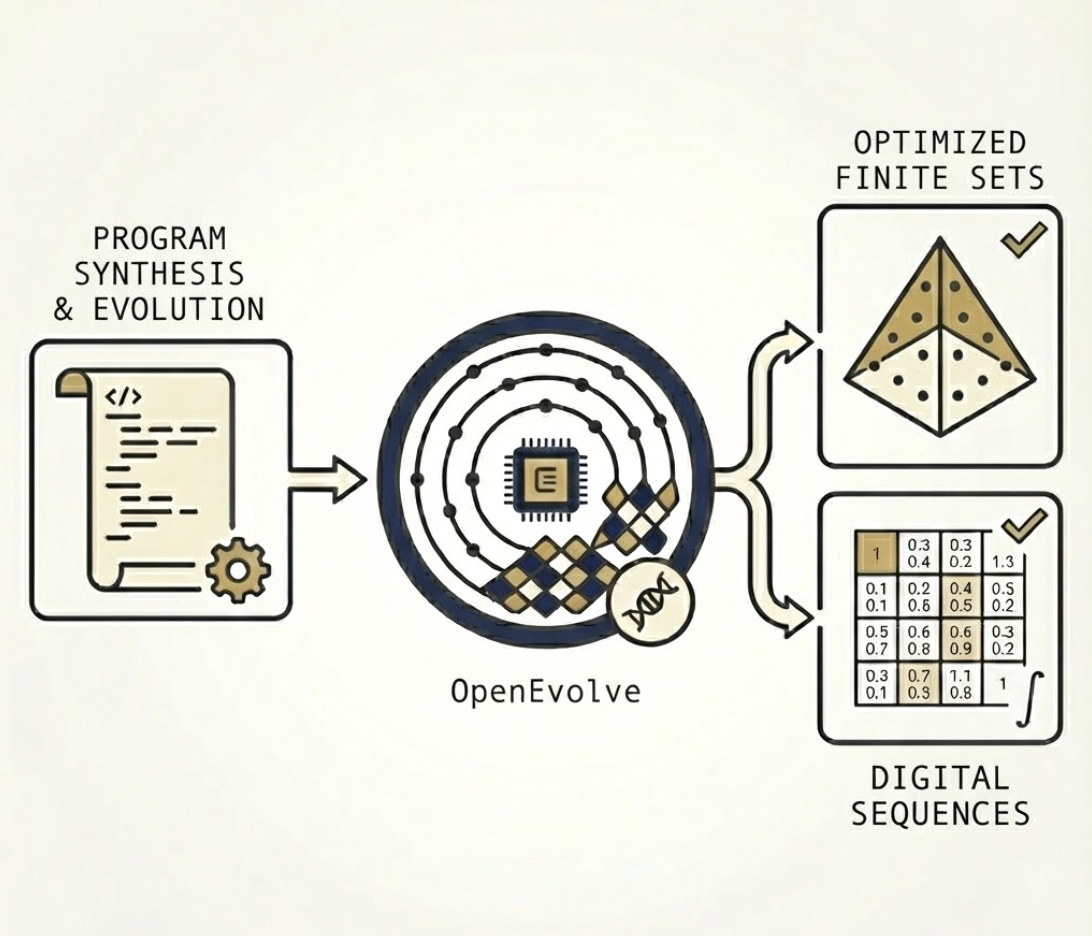
Quasi-Monte Carlo (QMC) methods generate "low-discrepancy" point sets — mathematical constructions that fill a multi-dimensional space more uniformly and consistently than the independent and identically distributed points used in standard Monte Carlo simulations. With these structured point sets, QMC allows researchers to solve complex integration problems (such as pricing financial options or simulating physical systems) with significantly lower variance, greater accuracy, and faster convergence. OpenEvolve helped advance this field by treating QMC design as a program synthesis problem: instead of humans manually tweaking formulas, an LLM-driven evolutionary search was used to write and refine code that generates these point sets. This approach successfully discovered new, record-breaking 2D and 3D point sets with lower "star discrepancy" (a measure of uniformity) than previously known configurations. Additionally, OpenEvolve optimized Sobol' direction numbers, which are the "instructions" for generating high-quality sequences; the resulting AI-evolved parameters significantly reduced error in 32-dimensional financial option-pricing simulations compared to long-standing industry standards, such as Joe–Kuo. Full details in the paper and code.
OpenEvolve for AI Driven Research for Systems (ADRS)

OpenEvolve for AI Driven Research for Systems (ADRS)

UC Berkeley's Sky Computing Lab used OpenEvolve as an open-source engine for AI-Driven Research for Systems (ADRS) to automatically discover and refine systems algorithms across multiple domains (for instance - MoE expert parallelism load balancer, multi-region spot scheduling, LLM-SQL preprocessing, transaction scheduling, and more). Reported results include up to 5× runtime speedups and double-digit percentage point cost reductions, often found within hours and sub-$20 evaluation budgets. Berkeley's team has documented their experience of using OpenEvolve and the results in their paper and blog.
OpenEvolve + GeoSpatial Knowledge ⇒ Improved Algorithms

OpenEvolve + GeoSpatial Knowledge ⇒ Improved Algorithms

Researchers from MIT and Stanford built GeoEvolve, a two-loop approach that combines an OpenEvolve-style evolutionary inner loop with an outer loop that retrieves and encodes geospatial domain knowledge ("GeoKnowRAG"). Applied to ordinary kriging (spatial interpolation) and geospatial conformal prediction (uncertainty quantification), GeoEvolve reports interpolation RMSE reductions of roughly 13–21% and interval-score improvements of about 17% on the evaluated datasets.
OptiLLM-Powered CePO: How Cerebras Turned Open Llama into a Fast, Test-Time Reasoner

OptiLLM-Powered CePO: How Cerebras Turned Open Llama into a Fast, Test-Time Reasoner

Cerebras has applied CePO, or Cerebras Enhanced Planning and Optimization, to the GPT-OSS-120B model through their inference endpoint. As an OptiLLM technique, CePO leverages test-time computation for iterative planning and refinement, all without retraining the model. CePO works as an inference-time pipeline tailored for Cerebras hardware, allowing the model to plan, iterate on solutions, and refine outputs in real time. As part of the OptiLLM framework, it breaks down complex tasks like code generation into steps: outlining a plan, generating multiple attempts, analyzing for consistency, and picking the strongest result. This uses more tokens overall but turns hardware speed into an advantage for better reasoning, something that is tough on standard setups due to memory limits. The approach builds on earlier work with Llama models and has been extended in updates to models like DeepSeek R1 and Qwen QwQ 32B.